Triangles. How tricky can a 3 sided shape be, really?
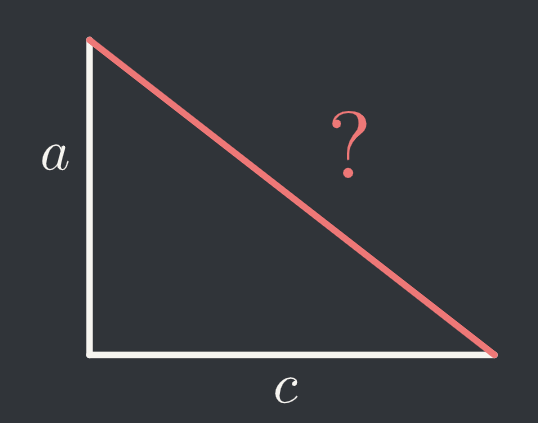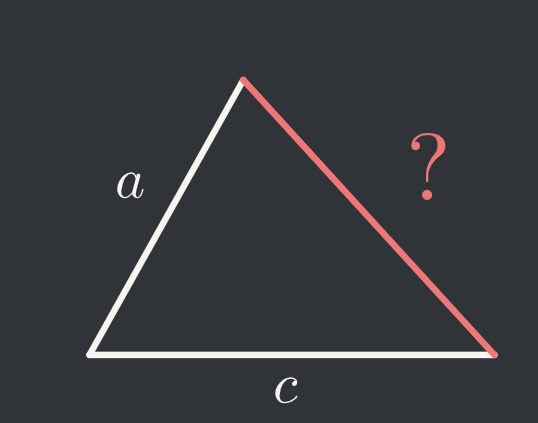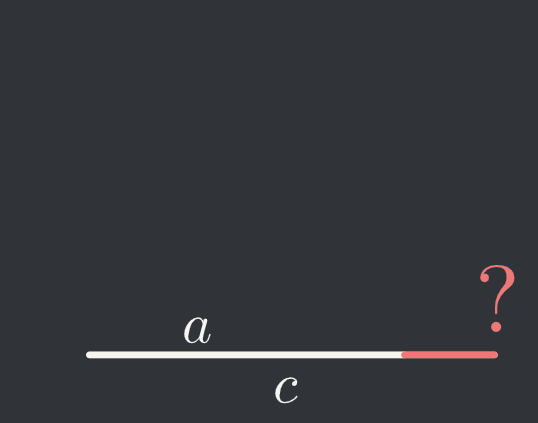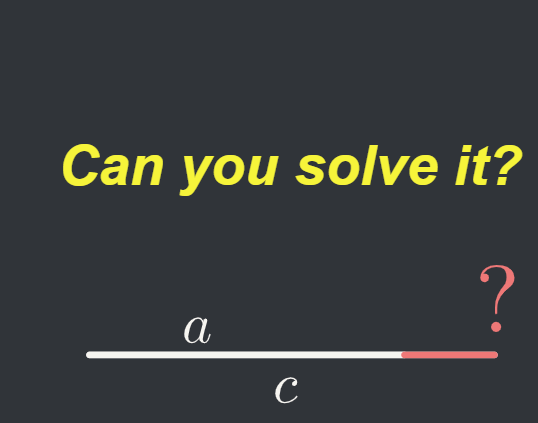
Table of Contents
- Problem
- Solution
- Commentary
- Problem References
The Problem
A triangle has whole number side lengths a, b, \text{ and } c , where a \leq b \leq c
How many such triangles are there if c = 9?
Can you find a formula for the general case – i.e. where c is an arbitrary positive whole number?
Solution
If c = 9 there are 25 such triangles.
The general case is \begin{aligned}&\left( \frac{c + 1}{2} \right)^2, \text{ \(c\) is odd} \\ &\left( \frac{c + 1}{2} \right)^2 – \frac{1}{4}, \text{ \(c\) is even} \end{aligned}
Below I’ll prove it. I was pleasantly surprised to find myself stumbling head first into the converse of the triangle inequality, and drawing a connection to the intermediate value theorem. Let me know in the comments how you solved it!
The Converse TIE
The triangle inequality (TIE) guarantees that a + b is strictly larger than c . i.e. Going around the block (a and then b) is a longer trip than taking c directly.

The triangle inequality is a math-ified representation of some very basic intuition. What is less intuitive is that the converse statement is also true.
Given 3 numbers, there exists a triangle with those numbers as side lengths exactly when the triangle inequality holds for all combinations of sides. In math speak, the TIE gives a necessary and sufficient condition to check if 3 rods determine a triangle.

The GIF below gives a visual of the situation. With two sides fixed, the third side varies continuously, and traces out all numbers in the allowable range (I was thinking more along the lines of the intermediate value theorem when I first approached this problem).

In any event, all that remains is to count.
The Final Count (Down)
Fix the longest side c at 9 units and use the TIE to find the possible lengths of a \text{ and } b:

Entries in red violate the TIE.
Entries in blue are duplicates of existing entries.
The converse TIE guarantees that the possibilities shown in the table really do form triangles. The fact that c = 9 is the longest side implies that there is no column left of, nor row below what the table shows. Any pairs that would fall in a column to the right of what is shown in the table are either duplicates, violate the TIE, or both. No entries with a number larger than 9 appear by hypothesis that 9 is the longest side.
By counting the number of valid side length pairs (a, b) in each column, we get the pleasant pattern 9 + 7 + 5 + 3 + 1 = 25, which solves the problem for c = 9 .
The general case follows the same logic. If c is an odd number, then add consecutive odd numbers. If c is an even number, then add consecutive evens. The formulae from the solution statement above capture the idea precisely.
Commentary
This is a Good, Low Bar Problem for School Math
- It’s nice to have a problem about whole number triangles that’s not about Pythagorean triples. Pythagorean triples seem to dominate the discussion at this level.
- A typical textbook exercise on the converse TIE presents a student with 3 numbers and asks if there exists a triangle with those numbers as side lengths. Like all good problems, what I appreciate here is how the problem naturally motivates the core idea. I mean this must be the only time I’ve used the converse TIE since high school.
Connections to higher level math?
This problem reminds me of other ideas I’ve seen in higher level math. The connection is this: Certain problems start off with distance data (how long are the side lengths of the triangle, how far apart are points in a cluster, etc.), and the problem is to determine some geometric properties of the shape from the distance data:
Rigidity theory – Used to model mechanical arms, or just ask cool geometry questions. How flexible is a structure constructed from rods that are connected to one another at joints? Since the rods are of fixed length, this is a question about distances.
Multidimensional Scaling – An algorithm in statistics/machine learning primarily used to make data visualizations. For high dimensional data sets, you can’t “see” the data as is, so you’d like to project it down to 2 or 3 dimensions and take a peek.
How to do this? The multidimensional scaling algorithm is built to preserve the distances between data points as best as possible, so that the visualization gives an accurate sense of which data points are close together or far apart in your data set.
I’m sure there are many more problems in combinatorics/geometry that are motivated by this basic question, but I’m no geometer.
Problem References
I found this problem in this problems book by esteemed mathematician (and verified Martian) George Polya.

Leave a Reply